Para terminar aplicaré Euler al caso particular de la esfera poligonada solamente con triángulos tal como lo desarrolla mi amigo Mariano Nieto.
En una esfera triangulada, cada cara tiene 3 aristas, pero como cada arista pertenece a dos caras, será:
3C / 2 = A
Según Euler, es:
C + V = A + 2 C = A + 2 – V
Combinando estas igualdades se tiene:
C + V = 3 C / 2 + 2
2C + 2V = 3C + 4
2V = C + 4
2V = A + 2 – V + 4
3V = A + 6
Con estas tres igualdades resaltadas en rojo se tienen las relaciones de cada dos de las tres variables C, V, A. Veamos si se satisfacen en nuestro caso.
Del cuadro de los triángulos correspondientes a la semiesfera deducíamos para ella estas cantidades:
C = 84 caras triangulares.
V = 49 vértices.
A = 132 aristas.
Estos valores, traducidos a la esfera completa se convierten en:
84 x 2 = 168 caras triangulares C.
49 x 2 – 12 = 86 vértices V.
132 x 2 – 12 = 252 aristas A.
Llevando estos valores a las ecuaciones rojas, se tiene:
3 x 168 / 2 = 252 = A
2 x 86 = 168 + 4 = 172 = C + 4
3 x 86 = 252 + 6 = 258 = A + 6
Efectivamente se cumplen las condiciones de esfera poliédrica triangularia.
Más arriba hablaba de dibujar la semiesfera con CAD 3D. Así lo hice; el resultado es la Fig. 15 que puede compararse con la 13.
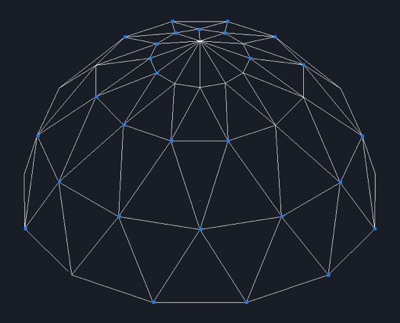
Fig. 15
Esta Fig. 15 me sirvió para, tomando medidas en ella, componer la 17 que es la esfera completa construida con sus caras triangulares de cartulina.
La Fig. 15 es el final del proceso CAD 3D. Las dos primeras fases de ese proceso se muestran en la Fig. 16 en la que se puede ver, a la izquierda, la primera pirámide ecuatorial con su vértice en el centro de la semiesfera. A la derecha se aprecia otra pirámide, la primera que se apoya en un paralelo.
Llegado aquí he querido comprobar sobre la Fig. 17 el cumplimiento del segundo teorema de Descartes relativo a poliedros. Ya hemos visto satisfecho el primero, conocido como de Euler (aunque antes ya lo había descubierto el propio Descartes).
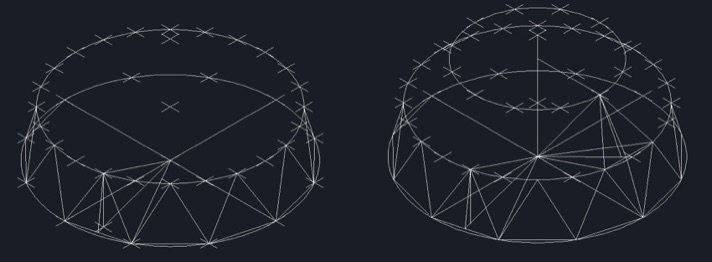
Fig. 16

Fig. 17