Ya tenemos la Fig. 3, la que necesitaba para construir la 2. Ésta va a consistir solamente en la estructura que contenga nada más que las aristas exteriores de la 3; para ello tenemos todo lo necesario: la longitud de todas esas aristas y su situación en el espacio, es decir, toda una serie de triángulos.
Estos serán según el siguiente cuadro.
Aplicando el teorema de Euler a este poliedro semiesférico (caras + vértices = aristas +2), será (C + V = A + 2):
[1 (el gran dodecalátero de la base) + 84 -triángulos aparentes totales-] + [(12 x 4 -los vértices contenidos en el ecuador y los tres paralelos-) + 1 (el polo)] = [12 x 4 + 12 x 2 x 3 + 12] + 2
85 + 48 +1 = 48 + 72 + 12 + 2
134 = 134
Es decir, descontando la base del suelo como cara, la cúpula tiene:
84 caras C.
49 vértices V.
132 aristas A.
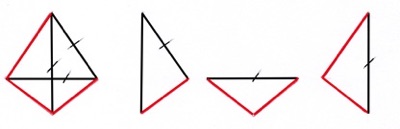
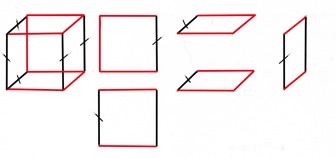
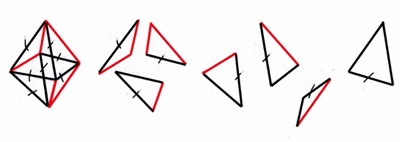
Llegado aquí quiero aprovechar la ocasión no para demostrar el teorema de Euler, sino para mostrarlo. Se trata de una especie de demostración por inducción de andar por casa, apoyada en los tres poliedros platónicos más sencillos (tetraedro Fig. 7; hexaedro Fig. 8; octaedro Fig. 9).
Las tres figuras son alámbricas. En los poliedros se destaca una línea roja quebrada en el espacio que pasa por todos sus vértices. Llamando Ar (Aristas rojas) a las contenidas en la línea quebrada, y An a las Aristas negras restantes, será:
A = Ar + An
Ar = V - 1
Las figuras se completan con las C–1 caras necesarias para recoger todas las An (An = C – 1). Esas caras aparecen dibujadas aparte como trasladadas, y en cada una está marcada la An que se corresponde con la del poliedro. Llevando esta constatación a las últimas igualdades, se tiene:
A = V – 1 + C – 1 es decir
A + 2 = C + V
El visionador atento ya se habrá dado cuenta de que, en realidad, la esfera de Jano no lo es del todo. Su mitad laminaria prácticamente sí es semiesférica, pero la alámbrica de la Fig. 2 lo es menos. Y la Fog. 1 lo acusa. Me ha salido un poco brunelleschi, un poco apuntada. Ello se debe, una vez más, a las inevitables licencias de construcción. La celosía esférica está hecha, en teoría con segmentos de línea recta. En la práctica, mis perfiles de cartulina son uves de 5 mm de lado. Al crecer desde el ecuador hasta el polo van acumulando exceso de altura indeseable que da lugar a su forma un poco picuda.
Además, la mezcla de fuerza y cariño que apliqué a la figura laminaria para llevarla a su ser teórico no he podido repetirla con la alámbrica porque es mucho más frágil que su compañera. De hecho, tuve que reforzar los elementos más sensibles al pandeo con uves interiores de menor ala. El resultado, después de todo, no es tan malo, verán.
La Fig. 3 es, en realidad, el andamiaje necesario para construir la 2, solo que no es necesario edificarla in situ y a tamaño natural. Basta un modelo de estudio a escala reducida cuyos elementos, debidamente escalados producirán los perfiles del tamaño real necesario para edificar. Naturalmente, el modelo reducido se puede conseguir con un programa CAD. Yo he preferido recurrir a entretenerme con estas maquetas cuya elaboración produce mucha satisfacción a la vez que estímulo de la creatividad para resolver las más variadas incidencias constructivas. Sin embargo, al final me decidí a dibujar la semiesfera con CAD.
Con lo que acabo de decir reflejo la gran dificultad a la que tuvo que enfrentarse Brunelleschi. Se llega a decir que no habría en toda la Toscana madera suficiente para construir el andamiaje convencional necesario para soportar la cúpula que había de construirse. Pero él la construyó; sin ese enorme andamiaje; recurriendo sólo a soluciones puntuales de ayuda al crecimiento de la obra de una manera que recuerda al encofrado deslizante. Y con su novedoso ingenio.
Fig. 7
Fig. 9
Fig. 8