LOS MISTERIOSOS CUADRADOS QUE SOBRAN (o faltan)

A mí, la magia me resulta admirable, y los magos, ya, ni les cuento. Además me creo a pies juntillas lo que veo que hacen; si pensara que detrás hay truco me desilusionaría tanto que, simplemente, prefiero disfrutar de las maravillas que contemplo.

Pero tengo que añadir que, tanto como el espectáculo mágico, me admira el hecho de que en tiempos de filtraciones como estos, donde hay un leak para cada cosa, se mantenga un secretismo invulnerable en torno al arte de la magia y sus trucos.

Cuando oigo decir a un mago, en el clímax de su presentación, que va a desvelar el truco, me dispongo a prestar la mayor atención a sabiendas de que, a cambio de no hacer lo prometido, nos va a sorprender con mayor arte.

Así pues, a riesgo de que los magos se enfaden conmigo, voy a intentar dar el soplo del truco que alienta detrás de estos juegos de los cuadrados desaparecidos; hay muchos de este tipo pero me voy a detener en unos que son bien distintos entre ellos y de mucho mérito.

PRIMERO

Partamos de un rectángulo de 5 × 10 cuadrados de lado 1 cm (Fig. 1). En él trazamos los segmentos AB, CD, EF y GH.

Cortamos por esos segmentos obteniendo 5 piezas. Según Fig. 2, las piezas 1, 2, 3, 4 y 5.

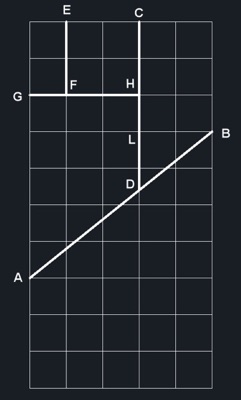
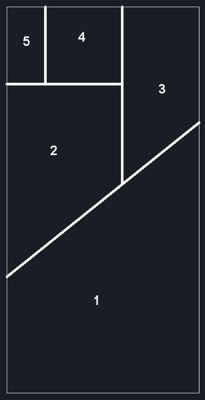
Fig. 1

Fig. 2

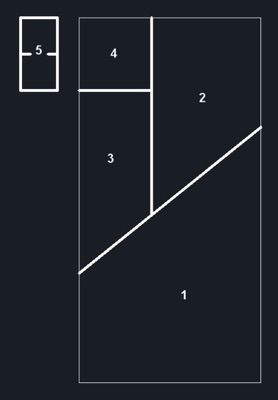
Fig. 3

A continuación se hace el truco consistente en componer la Fig. 3, con la misma base de las 5 piezas de la 2, pero organizando esas 5 piezas de forma distinta a la adoptada en la Fig. 2; el resultado es que sobra la pieza 5: misteriosamente han quedado fuera 2 cuadrados.

Lo que se ha hecho es deslizar a lo largo de AB las piezas 2 y 3 en posiciones alternadas en las figuras 2 y 3. Como el trapecio grande 1 queda invariable en ambas figuras 2 y 3, resulta que la altura de los rectángulos grandes viene determinada por la longitud de las bases pequeñas de los trapecios pequeños: 3 cm para la Fig. 2 y HD (que es menor de 3 cm), para la Fig. 3.

En la realidad, la Fig. 3 se produce por descomposición de la 2 de manera que no hay forma de verlas simultáneamente juntas para compararlas: ese es el gran truco que emplea la magia, el de la ilusión óptica. Aquí yo he procurado ponerlas separadas aunque se pueden ver simultáneamente.

Observando con cuidado las Figs. 2 y 3 (no confundir figuras con piezas), se ve que ambos rectángulos grandes tienen la misma base (5 cm), pero su área se diferencia en 2 cm 2 (los sobrantes). Por tanto sus alturas han de diferenciarse en 2 cm 2 / 5 cm = 4 mm (que la vista no apreciará si no está muy avisada, y menos recordará en la representación real).

Si nos fijamos en la Fig. 1 se ve que consta de dos trapecios iguales que tienen en común el lado AB de manera que las Figs. 2 y 3 conservan en común la pieza 1.

Por tanto, la diferencia de alturas entre los grandes rectángulos de las Figs. 2 y 3 es la misma que hay entre las bases pequeñas de los trapecios pequeños de las piezas 2 y 3 tal como se dijo antes. Veamos cuánto mide HD.

HD = 1 + LD

Tang (LDB) = LB / LD = 5 / 4

LD = (4 / 5) LB = 2 × (4 / 5) = 8 / 5

HD = 1 + 8 / 5 = 13 /5

Así pues, la diferencia que buscamos entre las alturas de los dos grandes rectángulos será:

3 – HD = 3 - 13 / 5 = 2 / 5 = 0,4 cm = 4 mm.

Esa altura 0,4 multiplicada por la base 5 produce el área 5 × 0,4 = 2 cm 2 que es precisamente la que da lugar al rectángulo sobrante 5 de la Fig. 3.

SEGUNDO

Éste es muy parecido al primero, solo que en vez de sobrar dos cuadrados, sobra uno solamente. Se parte de un rectángulo de 7 × 9 cuadrados de lado 1 cm (Fig. 4) del que se obtienen las piezas 10, 20, 30, 40, 41, 42 y 43.

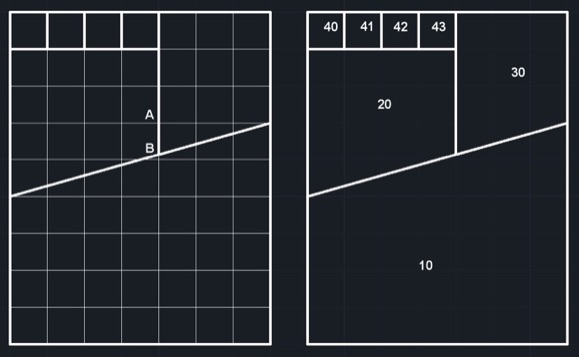
Fig. 4

En la Fig. 5 se han alternado las piezas 20 y 30 respecto de su posición en la Fig. 4 y queda como sobrante el cuadrado 43.

Naturalmente, este rectángulo de la Fig. 5 tiene una altura  un séptimo de cm menor que la de la Fig. 4 (un cuadrado sobrante de 1 cm2 / entre 7 cm de base = 1 / 7 de cm): una diferencia inapreciable en la distancia, y menos aún para ser recordada).

Averigüemos en la Fig. 4 la diferencia entre las bases pequeñas de los trapecios 20 y 30.

La base pequeña de la pieza 30 mide 3. La de la pieza 20 mide 2 + AB siendo AB / 2 = 3 / 7 (fijarse en los dos triángulos rectángulos semejantes).

Así pues hay que comparar 3 con 2 + 6 / 7 = 20 / 7. La diferencia será 3 – 20 / 7 = (21-20) / 7= 1 / 7 que es la misma que se apreció antes.

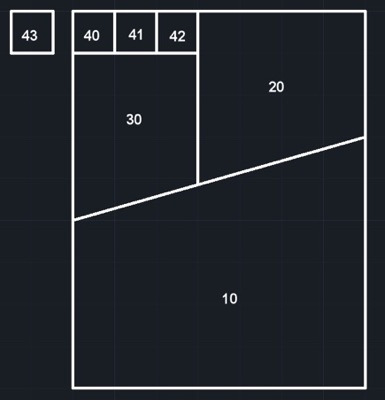
Fig. 5