Pgs. 1 2
Yo siempre he tenido una obsesión que podría calificar de esférica, porque considero a la esfera como resumen de perfecciones, destacando la de optimizar la relación volumen / superficie. Ya he dicho en otro artículo que la esfera procede del tetraedro originado en el Big-bang.
Si tomamos un tetraedro como el envolvente de la Fig. 1, resulta fácil triangularlo en todas sus caras para luego piramidizarlo de manera que las pirámides resultantes tengan por base los pequeños triángulos equiláteros faciales y por vértice común a todas ellas, el centro del tetraedro.
Tomando como origen de coordenadas al centro del tetraedro, se pueden obtener las tripletas de coordenadas de cada vértice de esas pirámides triangulares. Y conocidas éstas, obtener las seis distancias entre sus vértices con lo cual se pueden construir los desarrollos piramidales, componerlos y formar el panal tetraédrico.
En ese panal tetraédrico hay dos clases de pirámides componentes: Como Fig. 5 hay seis por cara, y como Fig. 6 hay una tripleta por vértice. Los lados de los desarrollos están redondeados a la unidad para un panal tetraédrico de radio igual a 50.
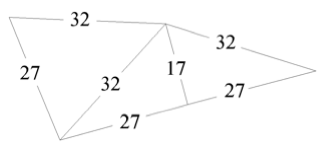
Fig.5
Fig.6
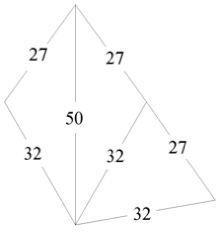
Y aquí vino la intervención de el monge. Por aquello de la larga y penosa evolución del tetraedro hacia la esfera, yo pensé que podría haber un atajo. Se trataría de proyectar sobre la virtual esfera circunscrita al tetraedro, todos los vértices del panal en que se había convertido dicho tetraedro.
Para lograr esa proyección contaba con las tripletas de coordenadas de todos los vértices del panal tetraédrico. Esas tripletas, ya asentadas sobre la esfera valdrían tanto como las tetraédricas pero afectadas en la proporción de distancias de los vértices correspondientes, al centro del tetraedro (que naturalmente, es el mismo que el de la esfera).
Así pues, todos los datos necesarios para la transformación estaban disponibles. Sólo faltaba confeccionar un sencillo programa en Quick Basic para hacer los cálculos con seguridad a partir de los datos recogidos de unos dibujos precisos desarrollados en Auto Cad.
A la figura resultante yo la llamé el avispo (en las Figs. 2, 3 y 4 se muestra el mismo volumen desde distintos ángulos) en honor de las sufridas avispas que tanto me ayudaron y que tuvieron la gentileza de no picarme nunca.
Como mi objetivo era materializar puntos de la esfera, he empleado sólo la cartulina imprescindible para conseguirlo. Así pues, el avispo, está hecho con dos clases de pirámides según las Figs. 7 y 8, y siempre para un radio de esfera de 50.
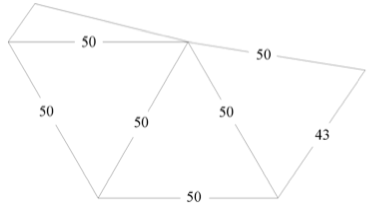
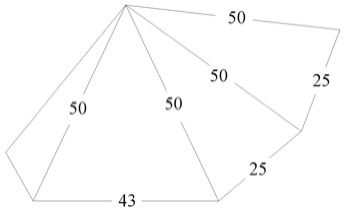
Fig.8
Para acabar y, dado que Monge y Euler fueron coetáneos, me gustaría aplicar el teorema de este último relacionado con los poliedros, orientándolo hacia las figuras que he venido manejando. Como se sabe, el famoso teorema se expresa como que “caras + vértices = aristas + 2” (C+V=A+2).
He añadido el Icosaedro platónico como elemento de comparación de vértices (puntos determinantes de la esfera circunscrita). En el Icosaedro platónico es V = 12, y en el Avispo, V = 44, lo que muestra la superioridad de este último. La verdad es que rueda que da gloria verlo.
Tetraedro platónico: C = 4; V = 4; A = 6 4+4=6+2
Panal tetraédrico: C = 36; V = 20; A = 54 36+20=54+2
Avispo: C = 84; V = 44; A = 126 84+44=126+2
Icosaedro platónico: C = 20; V = 12; A = 30 20+12=30+2
Las 36 caras del Panal tetraédrico son los nueve triángulos equiláteros planos de una cara del Tetraedro platónico, multiplicadas por 4 (las caras de éste último).
Es de notar que en el Avispo sólo hay triángulos isósceles con la excepción, explícita, de las cuatro tripletas de ellos que se corresponden con los vértices del Tetraedro platónico y que forman cuatro triángulos equiláteros (ver en el centro de la Fig. 2 uno de esos triángulos equiláteros).
En la Fig. 3 aparece uno de sus exágonos regulares (regular en su propio plano) que tienen todos los ángulos centrales iguales y menores de 60º (el lado es menor que el radio): es que son exágonos esféricos. Se pueden apreciar sus radios iguales al lado mayor del gran triángulo isósceles (el fundamental).
Asimismo se puede ver (Fig. 4) un pentágono con apariencia de regular, sin serlo. Es esférico, con cuatro lados iguales a los lados mayores del triángulo isósceles fundamental, y con su quinto lado igual al lado menor de ese triángulo fundamental, que resulta ser igual al del triángulo equilátero al que me referí dos párrafos más arriba.
En la Fig. 2 se ve también otro exágono esférico alrededor del mencionado triángulo equilátero.
He de advertir que como el avispo es una proyección del Panal tetraédrico debería tener, como él, 20 vértices; la realidad es que, mientras lo construía, pude añadirle otros 24 usando de simetrías (recuerden que había que ampliar el habitáculo de las avispas). Asimismo diré que en el avispo se cuentan como reales una aristas (y sus correspondientes caras) que son virtuales. Al final lo que resulta es un poliedro irregular que, como cabía esperar, no escapa al teorema de Euler, ya que éste es aplicable a todo volumen encerrado por caras, vértices y aristas ya tenga forma regular o irregular, e incluso configuraciones parciales cóncavas y convexas.
Pero lo más curioso de todo ello es que la Fig. 1 está, materialmente, dentro de las Figs. 2, 3 y 4.
Y aquí se acaba la historia; por favor, no se acerquen demasiado al avispero.
Bibliografía:
El primer naufragio, de Pedro J. Ramírez; editorial La Esfera de los Libros.
Fig.7
PAG. 2 / 2