
Pgs. 1 2
PERSECUCIÓN
Planteado a lo moderno, a lo cibernético, este problema sería algo así como:
En los vértices de un cuadrado de 100 Km de lado hay instalados sendos misiles que, marchando a la misma velocidad y, en el momento en que se les dé la señal de salida, partirán simultáneamente, cada uno en persecución del contiguo -en el sentido de las agujas del reloj: A seguirá a B, B a C, C a D y D a A-, hasta encontrarse. Todos explotarán en el centro del cuadrado; la pregunta es: ¿Qué distancia habrá recorrido cada uno en el momento de la explosión? ¿Qué tipo de línea será la de las trayectorias seguidas?
Como no disponemos de medios tan sofisticados, vamos a sustituir los misiles por cuatro chicos colocados en las esquinas del patio del cole, que es un cuadrado de 10 m de lado. En vez de lo cibernético, vamos a emplear el modo un dos tres al escondite inglés sin mover las manos ni los pies. Al primer pitido del monitor, los cuatro saldrán en persecución de su perseguido, y lo harán hasta oir el 2º pitido para detenerse. Seguirán a continuación nuevos pitidos que, al sucederse con relativa rapidez, determinarán en los chavales unos tramos de trayectoria prácticamente rectos. Al final, todos se encontrarán en el centro del patio.
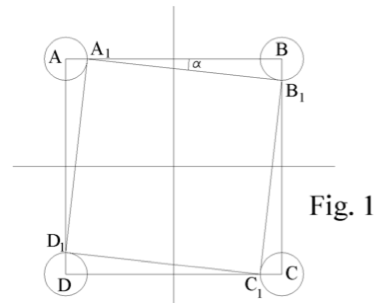
Supongamos que entre los dos primeros pitidos cada chico ha recorrido 1 metro (igual a AA1, BB1, CC1, DD1, es decir, la décima parte del lado del patio -(Fig. 1)-). Su situación en la primera detención es la de los vértices del cuadrado A1 B1 C1 D1.
Se ve que los chicos han pasado de los vértices del cuadrado inicial a los del 1, es decir, a un cuadrado que se ha contraído en la proporción de A1B1 / AB siendo
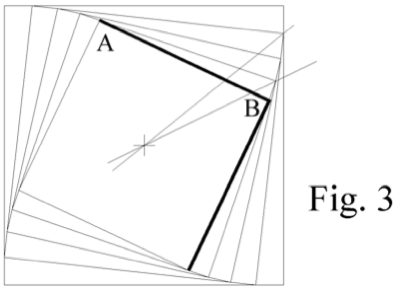
Como A1B = 9 y BB1 = 1, resultará
Siendo AB = 10, la contracción A1B1 / AB será de 0,90553851.
Se aprecia también que el cuadrado 1, además, proviene de un giro del cuadrado reducido, en torno del centro del patio, tal que
α= arc tan (1 / 9) = 6,3401917º
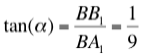
La otra particularidad que se observa es que, con las exigencias de contracción y giro, el cuadrado 1 tiene sus 4 vértices sobre el cuadrado original.
Operando sucesivamente como se acaba de ver, se consigue la Fig. 2 en la que se puede apreciar que los tramos de los recorridos van disminuyendo en longitud, debido a las contracciones sucesivas: El monitor tiene que acortar el tiempo entre pitidos.
El proceso para obtener dicha Fig. 2 será, pues:
- Copiar el último cuadrado que aparezca hacia el interior, con su centro, en un lugar aparte del plano.
- Allí, reducirlo de escala, con base en su centro, en la cuantía 0,90553851.
- A continuación, girarlo sobre su centro en el sentido de las agujas del reloj, 6,3401917º.
- Trasladar esta última figura para que su centro coincida con el del patio. Se verá que los vértices del nuevo cuadrado se asientan sobre los lados del anterior.
En la Fig.2 también se ve que las carreritas se van acortando hacia el centro que, teoríacamente, no se alcanzará nunca.
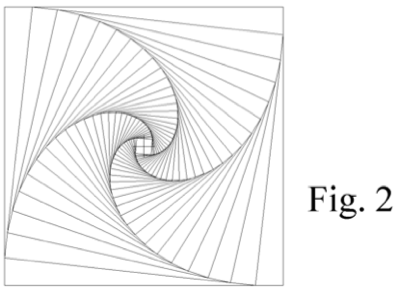
En la Fig. 3 se ve la posición que ocupan los chicos A y B en el último cuadrado interior después de la 4ª carrerita. En ella se aprecian cosas importantes:
- A mira siempre a B perpendicularmente a la trayectoria que va a seguir este último (líneas gruesas).
- AB es la tangente en A a la curva que describe A.
- Cualquier recta por el centro del patio corta a una curva (la que describe B) en un punto que es el vértice del ángulo de 45º formado por dicha recta y la tangente a la curva que describe A.
PAG. 1 / 2