Y para el simétrico de K = 2 (el antepenúltimo monomio)
Por ejemplo, para k = 2 (el tercer monomio), será
Comprobemos para n = 5, el valor del tercer coeficiente binomial que valía 10.
Lo primero que salta a la vista en este desarrollo es que para cualquier valor de n, tanto el primero como el último coeficiente binomial vale 1: igual que ocurre con los lados izquierdo y derecho del triángulo.
Asimismo se observa que los coeficientes binomiales del polinomio, al igual que se ve en el triángulo, resultan simétricos respecto del centro del polinomio. Ello es así porque siendo
Hasta aquí, el triángulo de Pascal, también conocido como de Tartaglia que parece haberlo descubierto unos cien años antes. El sabio italiano era apodado así por ser tartaja. Ya se ve que este triángulo resulta práctico para las potencias pequeñas, pero engorroso para las grandes.
Así pues, Newton, unos sesenta años después de Pascal estableció lo que después conocemos como binomio de Newton en el que los coeficientes binomiales son expresiones combinatorias de la potencia del binomio:
Pgs. 1 2
Si quisiéramos hallar el valor del monomio nº 31 en el desarrollo del polinomio (a + b)64, sería:
He puesto el ejemplo de n= 64 porque este valor es el límite del cálculo de factoriales en mi pequeña calculadora de bolsillo. En todo caso ya se ve la dificultad de hacer una operación como ésta con el triángulo de Pascal.
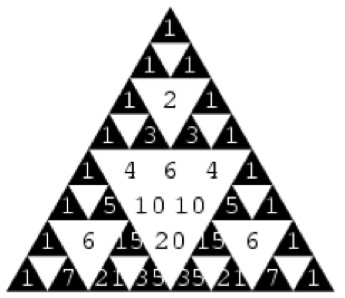
Terminaré volviendo al comienzo: El fractal Sierpinski puede acoger en sus triángulos a los elementos del triángulo numérico de Pascal o al combinatorio de Newton, con esta particularidad: Los números impares de Pascal se asientan sobre triángulos negros y los pares, sobre blancos (Fig. 4).
El monomio completo sería:
Fig.4
NOTA FINAL
Aún siendo tridimensional la Fig. 1, está hecha exclusivamente de triángulos equiláteros. Sin embargo, observándola con cuidado se aprecia la existencia en ella de 4 cuadrados pequeños y de uno grande (excusar la distorsión que introduce la perspectiva en la Fig. 5 en la que se destaca sólo uno de los cuatro). Ello hace pensar inmediatamente en octaedros que, una vez construidos dan lugar a la Fig.6.
Está hecha ésta con un octaedro grande (el lado de sus triángulos equiláteros es igual al doble del lado del tetraedrito) y con cuatro octaedros pequeños de lado igual al de dicho tetraedrito.
Como se ve, la Fig. 6 es una especie de negativo de la 1: Es, en macizo, lo equivalente a todo lo hueco que hay en la Fig. 1.
Al describir la Fig. 4 se apreciaba que los triángulos negros (los de los coeficientes binomiales impares) se correspondían con los triángulos llenos que la Fig. 1 muestra al exterior. Ahora podemos ver que los coeficientes binomiales pares se asientan sobre los triángulos equiláteros de la Fig. 6 (los que en la Fig. 1 están desaparecidos); no olvidar que los octaedros están hechos con triángulos equiláteros igual que los tetraedros y que en un octaedro, dos caras concurrentes en un vértice y que no se cortan en una arista, forman un ángulo igual al de dos caras de un tetraedro, es decir, 70,5288o.


Fig.6
Fig.5
PAG. 2 / 2