Pgs. 1 2
ProbLadrillos1
UN PROBLEMA DE LADRILLOS PARA MUDÉJARES
Todo Aragón, especialmente la provincia de Zaragoza y, no digamos, la de Teruel, está lleno de bellas muestras de arquitectura mudéjar cuya materia prima es el ladrillo. Nada más apropiado, pues, que brindar a ese arte con este problema.
Disponiendo de todos ladrillos iguales que se quiera, hay que apilarlos uno sobre otro y horizontalmente, dejándolos sueltos (sin argamasa ni nada parecido) atendiendo a dos condiciones:
1) Que la pila sea autoportante.
2) Que al final, la distancia proyectada sobre el suelo, entre extremos derechos del ladrillo de la base, y el más alto de la pila, pueda ser tan grande como se quiera (que esa distancia tienda a ∞).
Lo primero que se le ocurre a uno si se obsesiona con la condición 2) es poner el segundo ladrillo lo más a la derecha a fin de ganar distancia; la consecuencia es que, a poco que nos excedamos, se cae el mínimo apilamiento. Aún siendo conservadores, si se abusa, a los pocos ladrillos apilados, se cae toda la construcción.
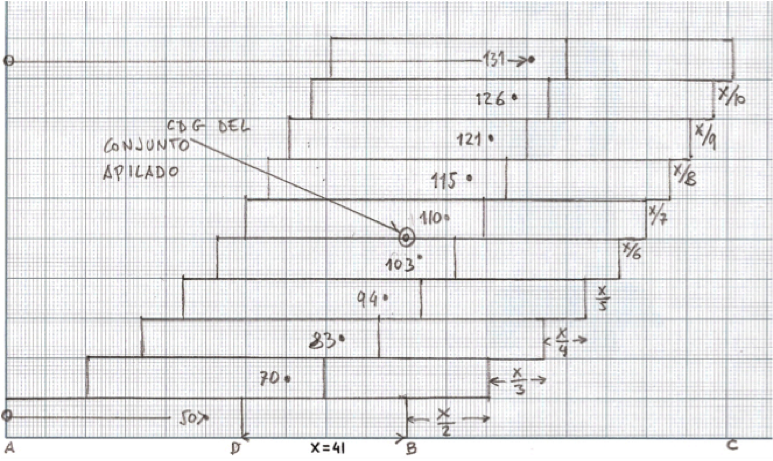
La condición 1) se traduce en que el CDG (Centro de Gravedad) del apilamiento terminado ha de estar en una vertical que pase por la base del primer ladrillo. Así pues, como mucho y, en el límite, esa vertical pasará por el extremo derecho del ladrillo base.
Inmediatamente nos damos cuenta de estar ante una paradoja: La masa de ladrillos apilada a la izquierda del plano vertical que contiene al canto derecho del ladrillo base debe ser igual o mayor que la masa apilada a la derecha de ese plano.
Parece, pues, que hay escaso margen de crecimiento de la pila hacia la derecha. Y sin embargo, ese crecimiento continuo que se ve en la figura debe y puede cumplir la condición 2).
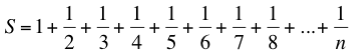
Dicho crecimiento hacia el infinito lo produce una serie, la conocida como serie armónica:
Esta serie es peculiar y paradójica: su término general tiende a cero cuando n tiende a infinito, y al mismo tiempo la serie es divergente.
La serie armónica se llama así porque cada término es la media armónica de sus dos adyacentes. Recordando que media armónica de varios números es el valor recíproco de la media de los recíprocos de esos números, se tiene, por ejemplo:
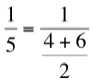
Pero no es eso sólo. Porque el adjetivo armónica nos lleva inmediatamente a pensar en la música.
Copio del libro de Marcus du Sautoy La música de los números primos (Ed. Acantilado):
El origen del interés de los matemáticos por esta suma infinita procedía de la música, y se remontaba a un descubrimiento realizado por los antiguos griegos. En realidad, Pitágoras había sido el primero en determinar el nexo fundamental que liga matemática y música. Había llenado de agua un recipiente y lo había percutido con un pequeño martillo para producir una nota. Al retirar la mitad del agua y percutir de nuevo el recipiente, la nota había subido una octava. Cada vez que retiraba agua de manera que quedara un tercio, un cuarto, y así sucesivamente, las notas que se producían sonaban en su oído en armonía con la primera nota que había obtenido. Cualquier otra nota que se obtuviera retirando del recipiente una cantidad distinta de agua resultaba disonante con respecto a la nota original. Estas fracciones poseían una belleza que podía ser escuchada. La armonía que Pitágoras había descubierto en los números 1, ½, 1/3, ¼, … lo indujo a creer que el universo entero estaba controlado por la música, y por esta razón acuñó la expresión “la música de las esferas”.
Por otra parte, la demostración de que la serie armónica es divergente, es clásica, conocida, sencilla y elegante. No me resisto a transcribirla:
Si en la serie armónica S que escribimos antes hacemos las dos agrupaciones entre paréntesis
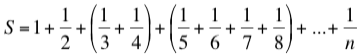
tendremos pie para escribir esta nueva serie
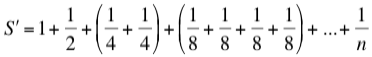
y para observar que S´< S gracias a las sustituciones hechas. Como
crece indefinidamente, con mayor motivo crecerá S, también indefinidamente, al ser mayor que S´.
Se ve, pues, que el problema tiene una base teórica que debe conducir a una ejecución práctica: no podemos disponer de una cantidad infinita de ladrillos y, de tenerlos, no podríamos apilarlos, así que vamos a ser prácticos. En la figura nos hemos conformado con apilar n = 10 ladrillos de longitud l = 100 y altura h.
Si tomamos al pie de la letra la serie armónica, habría que asociar la unidad a la longitud del ladrillo base, arrastrando el segundo ladrillo hacia la derecha hasta que vuele su mitad derecha. Pero ya hemos dicho antes que ese proceso es inviable.
Habrá que encontrar un valor x que hará de unidad, para sobre esa unidad construir la serie armónica; x habrá que calcularlo en función de l, de n y de la condición de que el CDG del apilamiento esté en la vertical por B. Generalizando, tendremos que el momento de cada ladrillo respecto a la vertical por A, desde el más bajo al más alto, vale:
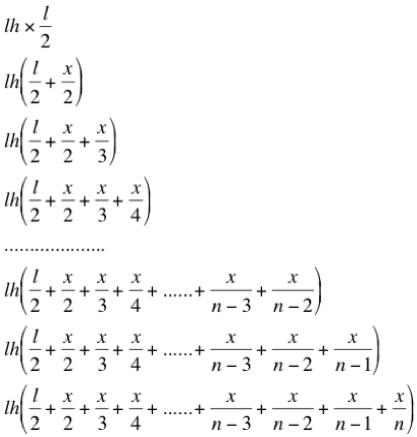
La suma de momentos valdrá:
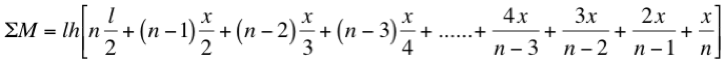
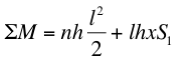
siendo
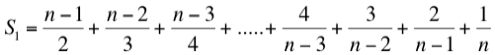
Condición para que el CDG del conjunto de n ladrillos apilados caiga sobre el extremo derecho del ladrillo base:
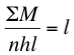
Igualando los dos valores de M tenemos:
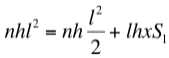
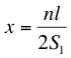
Olvidémonos de sumar la serie S1 y limitémonos a sumar sus 10 primeros sumandos.
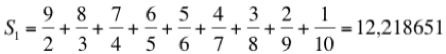
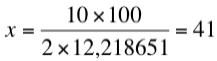
PAG. 1 / 2