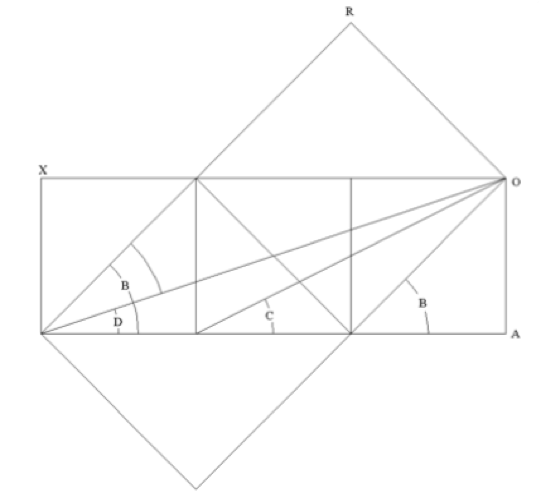
Sean los tres cuadrados de la fig. superior. Demostrar que con los ángulos marcados en el lado inferior del rectángulo se cumple que el ángulo marcado en B es la suma de los marcados en C y en D.

Transportamos esos 3 ángulos como alternos-internos al vértice O. Allí se ve que

ang.B = ang.C + un ang. sin identificar (que se comprueba como B – C al ser B un ángulo exterior en el triángulo OCB).

Si probamos que ese ángulo sin identificar vale D habremos demostrado lo que se nos plantea.

Si efectivamente ese ángulo vale D, por simetría, debe ocurrir que las bisectrices de los ángulos DOC y XOB coinciden. Y es esto lo que vamos a probar a continuación.

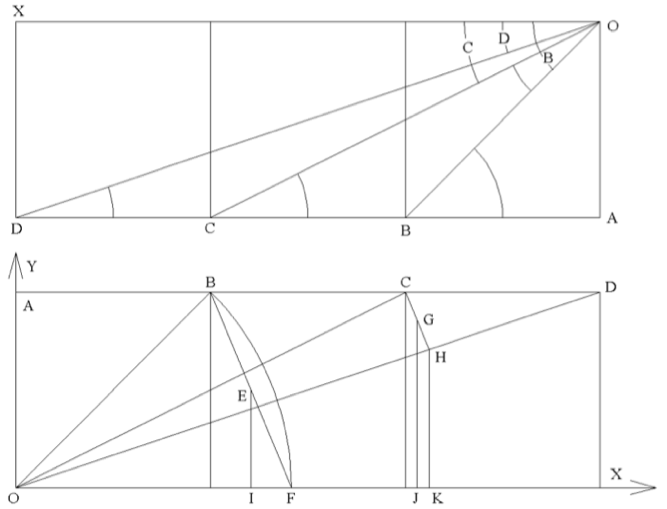
Por comodidad, damos vuelta a la figura superior para obtener la inferior, y tomamos el lado de cada cuadrado como unidad.

Ya en la figura inferior, se ve que E, punto medio de BF ha de estar en la bisectriz de BOX. Con una construcción semejante se llega a que G, punto medio de CH estará en la bisectriz de COD.

Como ambas bisectrices pasan por el origen O, si son coincidentes, han de tener la misma pendiente.

Para la pendiente primera será p1 = EI / IO

En el caso de la segunda, es: p2 = GJ / JO.

Las coordenadas de E son la media de las de B y F.

Siendo B (1 ; 1) y F (√2 ; 0), será E [(1 + √2) / 2 ; 1 / 2], así que la pendiente p1 valdrá:

p1 = 1 / (1 + √2)

C tiene por coordenadas (2 ; 1).

En cuanto a las de H, teniendo en cuenta que OH = OC = √(22 + 1) y observando los triángulos semejantes ODX y OHK, tendremos:

HK / DX = OH / OD          ;     HK = OH * DX / OD = √(22 + 1) / √(32 +1) = 1 / √2

OK / OX = HK / DX          ;     OK = 3 * HK = 3 / √2

Así que será H (3 / √2 ;1 / √2 )

La media de C y H da para G:

G [(1 / 2) * (2 + 3 / √2) ; (1 / 2) * (1 + 1 / √2)]

Con lo que la pendiente p2 de OG vale

p2 = (1 / 2) * (1 + 1 / √2) /  (1 / 2) * (2 + 3 / √2) = (1 + √2) / (3 + 2 √2)

Fácilmente se puede comprobar que este valor de p2 es el mismo que el hallado antes para p1 que es lo que se quería demostrar.

Hoy es 23-5-10 y ayer mismo moría Martin Gardner, el sabio y curiosísimo filósofo americano aficionado a las matemáticas (además de a otras muchas cosas).

Mi amigo Mariano me había propuesto el anterior problema procedente, precisamente, de M. Gardner. Yo lo he resuelto como he podido.

Todos los problemas suelen tener varias soluciones, pero la de Gardner no sólo es genial sino elegante y simple en extremo, lo que la hace más valiosa aún. No me resisto a copiársela a mi amigo.

En la siguiente Fig. se ve que B = D + un ángulo sin identificar. Pero resulta que este ángulo es igual a C: ambos son los formados por una diagonal y el lado mayor de sendos rectángulos semejantes, compuestos cada uno por dos cuadrados, y con razón de semejanza 2 (lados menores respectivos, OA y OR).