Este interés mío se debe a que durante la construcción de la esfera no he tenido más remedio que vivir muy de cerca este segundo teorema que se enuncia así:

En todo poliedro convexo la suma de los defectos angulares de todos sus vértices, o sea, el defecto angular total, es siempre igual a 720 o, equivalente a 4π.

Al construir los casquetes polares (Fig. 18) es donde mejor se acusa el efecto del defecto angular. Estos casquetes son lo equivalente a la clave de un arco. Por bien calculadas que estén sus dovelas, al llegar a la clave es casi seguro que habrá que retocarla para su buen encaje, debido a los defectos acumulados en la construcción del arco.

En mi caso, ambos polos tenían que distar 180 (recordar que el radio de la esfera era de 90. Sin embargo, los defectos acumulados hacían que si en la Fig, 18 el defecto angular era grande, la esfera resultaba picuda, pero de ser pequeño, quedaba achatada. Naturalmente, los polos son vértices de la esfera.

El resultado óptimo, y próximo al teórico, fue un casquete (en realidad una pirámide de base dodecalátera) compuesta de 12 triángulos isósceles iguales de lados 13 × 26 × 26.

En la Fig. 18 que es el desarrollo del casquete se aprecia bien cual es el defecto angular (que se utiliza para la pestaña de unión). Su valor es la diferencia entre 360o y la suma de los 12 ángulos menores de los triángulos isósceles.

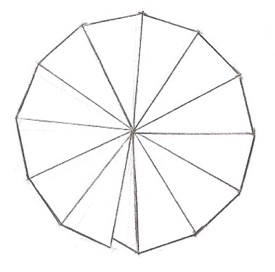
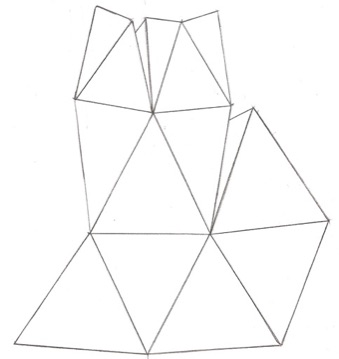
Fig. 18

Fig. 19

La Fig. 19 representa uno de los 6 conjuntos que, junto con la Fig. 18 llenan una semiesfera. En dicha Fig. 19 se pude medir el defecto angular de dos vértices: los afectados por las dos pestañas que se muestran.

Para calcular el defecto angular del vértice polo sólo necesitamos conocer el ángulo menor de los triángulos isósceles. Sin embargo calcularemos los tres ángulos porque los otros dos son necesarios para el cálculo de los defectos angulares de los vértices situados en el círculo polar.

Sabemos que, conocidos los tres lados a, b , c de un triángulo, sus ángulos opuestos vienen dados por:

α = arc cos [(b2 + c2 – a2) / 2bc]

y análogamente β y γ. Así pues, será:

α = arc cos [(262 + 262 – 132) / (2×26×26)] = 28,9550o

Defecto angular del polo = 360 – 12 α = 12,5397o

Calculemos ahora el defecto angular de los vértices restantes. Siguiendo el procedimiento anterior podremos dejar bien definidos todos los triángulos.

La cantidad de estos, que son las únicas superficies que cubren la esfera, es 168 = C. De ellos sólo hay 24 equiláteros ( de lados 46,5 × 46,5 × 46,5 y ángulos de 60o), los que asientan una base en el ecuador. Todos los demás son isósceles, habiéndolos de cinco clases diferentes determinadas por las longitudes de sus lados:

Llamaremos de la siguiente manera a las cuatro circunferencias en que la esfera es cortada por planos perpendiculares a su eje polar:

-Ecuador.

-Paralelo ecuatorial.

-Paralelo intermedio.

-Círculo polar.

-En los 12 vértices del ecuador concurren 6 ángulos de triángulo:

     4 de 60o y 2 ángulos pequeños de la Clase A: Total ≡ 4 × 60 + 2 × 53 = 346º

     Defecto angular de esos 12 vértices = 12 (360 – 346) = 168o

-En cada uno de los 12 vértices de un paralelo ecuatorial concurren también 6 ángulos de triángulo: 4 ángulos grandes de la clase A; un ángulo pequeño de la clase B y uno de 60o.

Total ≡ 4 × 63,4957 + 34,3989 + 60 =348,3817o

     Defecto angular de los 12 vértices = 12 (360 – 348,3817) = 139,4196o

-En cada uno de los 12 vértices de un paralelo intermedio concurren asimismo 6 ángulos de triángulo: Uno pequeño de la clase A; 2 grandes de la clase B; 2 grandes de la C y un pequeño de la D.

Total ≡ 53 + 2 × 72,8005 + 2 × 65,3757 +22,7196 =352,072o

     Defecto angular de los 12 vértices = 12 (360 – 352,072) = 95,136o

-En cada uno de los 12 vértices del círculo polar concurren sólo 5 ángulos de triángulo: 2 grandes de la clase D; uno pequeño de la C y 2 grandes de la E.

Total ≡ 2 × 78,6402 + 49,2486 +2 × 75,5225 = 357,574o

     Defecto angular de los 12 vértices = 12 (360 – 357,574) = 29,112o

-El defecto angular del polo ya fue calculado como 12,5397o.

Así quedan calculados los defectos angulares e una semiesfera. Los de la esfera completa serán los del ecuador más el doble de los restantes hallados para una semiesfera:

168 + 2(139,4196 + 95,136 + 29,112 + 12,5397) = 720,4146o

Recordamos que el valor teórico es 720o = 4π radianes. Hay que anotar el error de redondeo en las mediciones 3D de CAD.

Una vez mostrada la adecuación con el segundo teorema de Descartes de la esfera construida, veamos la demostración de éste mediante la generalización del proceso seguido.

Se ha visto que los defectos angulares de todos los vértices no son iguales debido a sus distintas configuraciones.

Llamemos Di al defecto angular del vértice i; será D = Σ Di el defecto angular total del poliedro esférico con C caras, V vértices y A aristas.

Tal como se ha visto antes, será:

Di = 2π - Si

Siendo Si la suma de los ángulos concurrentes en el vértice i, medida en grados.

Llamando S a la suma de todos los ángulos de todas las caras del poliedro (esférico en nuestro caso, pero simplemente convexo en general –poliedro convexo es aquel en el que se pueden unir dos vértices con una recta sin atravesar ninguna cara-), tendremos: