Pgs. 1 2
REVISTA DE CIENCIAS Y HUMANIDADES DE LA FUNDACIÓN RAMÓN ARECES
Nº 1, Enero 2010
Aparte de otros contenidos, recoge cinco conferencias dictadas en su sede. De entre ellas, me voy a fijar en dos dada su solvencia y su proximidad a mi preocupación por los límites del crecimiento.
TÍTULO DE LA CONFERENCIA:
El futuro de la desigualdad. Una perspectiva histórica (conferencia en inglés)
CONFERENCIANTE:
Jeffrey Gale Williamson, profesor emérito de la Harvard University, EE.UU.
Hace historia de las desigualdades sociales desde el Imperio Romano hasta nuestros días para poder analizar mejor lo que acontece en estos y así aventurar una visión de futuro.
Yo voy a poner entre paréntesis la historia para situarme en los tiempos que corren. Cuando el profesor Williamson habla de desigualdades no divaga como los demagogos; las cuantifica de acuerdo con el coeficiente de Gini. Por eso vamos a ver en primer lugar en qué consiste éste.
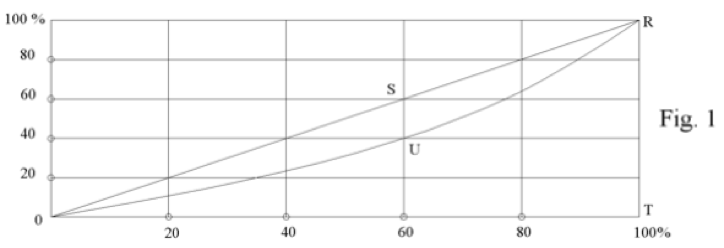
Gini (1912) fue un economista que, siguiendo los pasos de Pareto (1906; su cuantificación 80/20: el 80% de los efectos están producidos por el 20% de las causas -por ejemplo, el 80% de las ventas van a parar al 20% de los clientes-) y, utilizando la curva de Lorenz (OUR, Figs. 1 y 2) definió así su coeficiente:
G = A / (A + B)