
GOTAS DE ARTEUNO
Quisiera anotar ahora la complicidad del arte con la geometría, que es cosa constante en mis convicciones. Ya sé que con ello no descubro nada ni a los arquitectos ni a los pintores; a los primeros, por razones obvias y a los segundos porque saben hacer arte con otras materias primas además de las que implican las geometrías: la pintura impresionista, por poner un ejemplo, tiene poco de geometría a no ser por la ayuda que la perspectiva pueda prestar al conjunto.
Cuando he hablado de geometrías, me estaba acordando de un profesor mío que en un examen de geometría (no sé muy bien si se trataba de descriptiva o proyectiva) puso al pie del gran dibujo que le presentó el alumno, la siguiente anotación: “Estado en que quedó el convoy después del accidente”. El estado en cuestión era un amasijo de rectas que si bien no resolvían el problema, podrían muy bien haber sido fuente de inspiración para un pintor imaginativo.
Me voy a referir a lo que pueden dar de sí como vehículos de belleza ciertos rectángulos. En mi hablo de estos: el áureo o áurico, el homotómico, el argéntico y el cordobés. Del primero apenas digo nada, pero además veo que faltan, al menos, dos más que he descubierto hace poco. Como suele ocurrir, estoy seguro de que ya los habrán descubierto otros antes, pero no importa: me apresuraré a patentar sus nombres, por si todavía no los tienen.
Ahora no entraré en demostraciones geométricas ni en explicaciones pormenorizadas. Las daré por sabidas aunque no sea imprescindible conocerlas para saborear lo que mostraré luego. El curioso puede acudir a estos enlaces:
http://divulgamat.ehu.es/weborriak/Cultura/papiroflexia/Ficheros/jesus_pena_06_01.pdf
El rectángulo áureo (Fig. 1) es aquel cuyos lados están en la proporción áurea (1,618034, la misma que relaciona lados y diagonales de un pentágono regular convexo). En realidad, los 58º de la figura son 58,282527º. Este rectángulo ya me había servido para componer el bloque de diedros trirrectángulos de la Fig. 2.
Asimismo conseguí mostrar cómo un icosaedro puede envolver por completo al bloque áureo. En la Fig. 3 se ve que los 12 vértices de los triángulos equiláteros de las caras del icosaedro coinciden con los 12 vértices de los 3 rectángulos del bloque.
Salí luego del icosaedro para obtener la Fig. 4 en la que se ve que dos bloques áureos se pueden unir mediante triángulos equiláteros. Naturalmente, ello da pie a construir todas las uniones semejantes a la mostrada para configurar algo así como las macromoléculas de los polímeros.
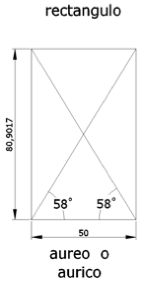
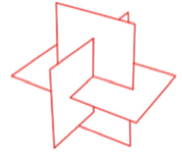

Fig.1
Fig.2
Fig.3
Fig.4

Un paso más. Vista la relación entre un bloque áureo y un icosaedro y sabiendo que el icosaedro y el pentágono-dodecaedro están relacionados, ¿cual podría ser la relación entre este último y el bloque áureo?
Nota. En lo sucesivo seguiré insistiendo en la denominación pentágono-dodecaedro sin reducirla a simple dodecaedro, porque hay otros dodecaedros sin caras pentagonales (el rombo-dodecaedro, p.e)
En la Fig. 3, puramente icosaédrica (toda triángulos equiláteros), aparece un pentágono que da la clave de esa relación. Consideraremos ese pentágono, hecho de lados de triángulos equiláteros, como siendo el pentágono de las diagonales de las caras pentagonales de un pentágono-dodecaedro. La relación de homotecia que se da en este poliedro nos permite hallar la longitud del lado del pentágono-dodecaedro buscado. El lado del pentágono-dodecaedro es igual al del icosaedro (que es igual, a su vez, al lado menor del rectángulo áureo), dividido por 1,618034.
La Fig. 5 es igual que la 2 después de conseguir que el bloque áureo esté en la situación que se muestra: la diagonal de un rectángulo queda en posición vertical.
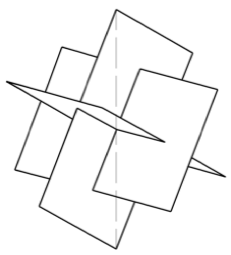
Fig.5
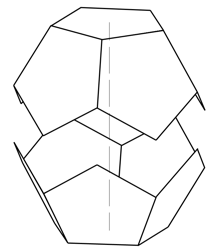
Fig.6
La Fig. 6 está hecha de dos semi pentágonos-dodecaedros con los centros de sus bases coincidentes con los extremos de la diagonal del rectángulo áurico. Obsérvense estas dos cosas: esas dos bases están giradas una respecto de a otra, 36º, tal como ocurre entre caras opuestas de cualquier pentágono-dodecaedro. Las dos mitades dodecaédricas están dispuestas de tal manera que si se deslizara la superior hacia abajo a lo largo de la diagonal del rectángulo, esas dos mitades coincidirían para completar la figura del pentágono-dodecaedro.
En la Fig. 7 aparece el bloque áurico metido dentro de las dos mitades dodecaédricas en forma cuasi transparente. En ella se aprecian estas coincidencias de vértices: las de ambos extremos de la diagonal con los centros de las bases pentagonales; las de otros 7 vértices, de rectángulos y pentágonos. Los 3 ocultos también son coincidentes.
Un pentágono-dodecaedro tiene 5 ⨯ 12 / 3 (cada tres caras comparten un vértice) = 20 vértices, pero en el caso de la Fig. 6 hay que descontar los 10 de la cintura media que no llegan a consumar la unión, así que quedan 10 (recordar que el lado del pentágono es más pequeño que el del triángulo equilátero del icosaedro de partida). Esos diez son los mismos 10 del bloque áurico cuando de sus 12 vértices descontamos los dos empleados en la fijación a los pentágonos base.
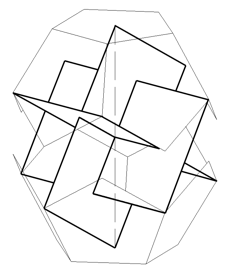
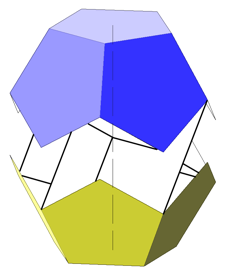
Fig.7
Fig.8
La Fig. 8 muestra cómo se verían desde el exterior los tres conjuntos ensamblados.
PAG. 1 / 3