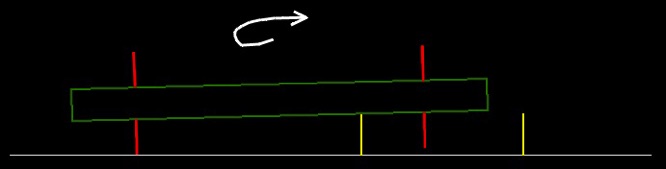
Fig. 6
Visto lo problemático de esta última experiencia, recurrimos a la Fig.6 en la que se producen sendos apoyos sin ninguna duda, positivos: C apoya su R izquierda en el suelo mientras que c se apoya en el borde izquierdo de la caja; la otra R queda al aire.
Así, C ya puede avanzar girando, pero, ¡atención!, el avance no se produce en línea recta sino en modo circular según indica la flecha y como si se tratara de un cono apoyado en una generatriz al que se hace girar en torno a su vértice. Es la manera de conseguir que la circunferencia base de un cono y otra coaxial y paralela a ella, puedan girar dando las dos el mismo número de vueltas.
Si insisto en hacer avanzar C en línea recta, puedo conseguirlo, pero a costa de arrastrar C (sin giro alguno) deslizándolo, respectivamente, sobre el borde de la caja y sobre el suelo.
En el caso (1) ocurre lo mismo que acabo de describir: es imposible el avance con giro de C, pero sí el avance por arrastre, con deslizamiento. La pretensión de avance por medio del giro de C exige que un mismo giro se sustancie, a la vez en dar una, y n vueltas, cosa que es un contradictio in términis, vamos, un oxímoron, para entendernos. Es algo así como pretender que los conos de un molino de aceite se comporten al mismo tiempo como si fueran los cilindros de una apisonadora.
Los más famosos matemáticos se han complicado la vida con esta cuestión. Cantor, por ejemplo (1845-1918), demostró que el cardinal de un segmento, o transfinito, es siempre el mismo y lo llamó continuum (Pickover).
A mí, que no voy tan lejos, me basta con el refrán castellano “Dos ideas de impar opinión no caben en el mismo zurrón”.
Lo asombroso es que esto ocurra con Aristóteles, el inventor del Principio de Contradicción: Una cosa no puede ser algo y su contrario.
ACLARACIÓN
Siempre cabe la objeción de decir: “La rueda grande rueda sobre su carril y simultáneamente la pequeña, solidaria de la grande, no tiene mas remedio que girar también pero, simultáneamente al giro también se arrastra”.
……….
La objeción no tiene solidez porque si la rueda pequeña se arrastra, la grande también se arrastra exactamente en la misma medida puesto que son solidarias. Por arrastre compensatorio nunca se podrá conseguir que α R = α r porque lo que hace es añadir la misma cantidad a los dos miembros de esa errónea igualdad.
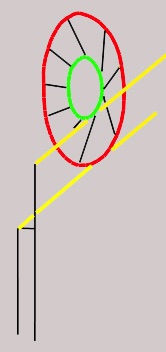
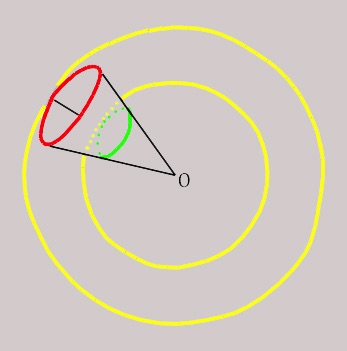
Fig. 7
Fig. 8
La Fig. 7 muestra lo que no se ve en la 1: que las dos ruedas son las bases de un tronco de cono. Y pretende hacer ver algo coincidente con dicha Fig. 1. Que el tronco de cono avanza girando sobre dos carriles rectos y paralelos, cosa que no es cierta porque contradice a la realidad. Ello se ve claro en la Fig. 8.
Dicha Fig. 8 es una vista en picado de un cono (en el que se destaca un tronco) asentado en un plano a todo lo largo de una de sus generatrices. Girará en torno al eje perpendicular al plano por O. El camino a seguir por las dos ruedas es la pareja de circunferencias concéntricas de centro O. ¡Nada de caminos rectos!
Para conseguir que esos caminos curvos se hicieran rectos y paralelos sería preciso que O fuera el punto del infinito del eje del cono, es decir, que el cono se convirtiera en un cilindro: con ello las dos ruedas serían iguales, y nos habríamos salido del ámbito del problema. Así se pone de manifiesto la imposibilidad de convertir el molino giratorio en una apisonadora que marcha en línea recta.
La Fig. 8 muestra otra anomalía: Las bases del tronco de cono no son perpendiculares al plano de los caminos, pero es fácil conseguir que lo sean. Basta con elevar O a lo largo del eje de giro tanto como lo necesario para conseguir que el giro del cono se produzca, no sobre el plano inicial, sino sobre una nueva superficie cónica que tenga la misma generatriz que el cono mostrado.
Si se insiste en los caminos rectos, las dos ruedas han de tener pestañas y deben ser arrastradas sin girar.